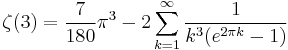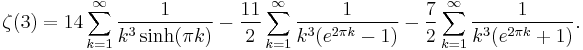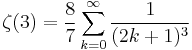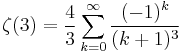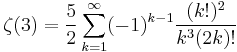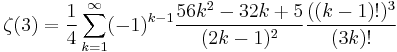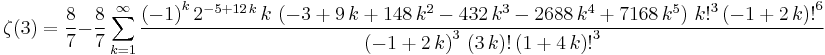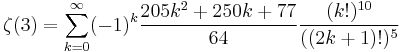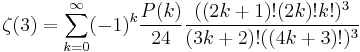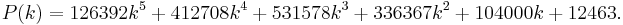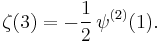Apéry's constant
| List of numbers – Irrational and suspected irrational numbers γ – ζ(3) – √2 – √3 – √5 – φ – ρ – δS – α – e – π – δ |
|
| Binary | 1.001100111011101... |
| Decimal | 1.2020569031595942854... |
| Hexadecimal | 1.33BA004F00621383... |
| Continued fraction | 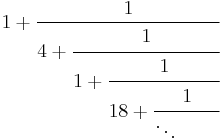 Note that this continuing fraction is not periodic. |
In mathematics, Apéry's constant is a number that occurs in a variety of situations. It arises naturally in a number of physical problems, including in the second- and third-order terms of the electron's gyromagnetic ratio using quantum electrodynamics. It also arises in conjunction with the gamma function when solving certain integrals involving exponential functions in a quotient which appear occasionally in physics, for instance when evaluating the two-dimensional case of the Debye model. It is defined as the number ζ(3),
where ζ is the Riemann zeta function. It has an approximate value of (Wedeniwski 2001)
- ζ(3) = 1.202056903159594285399738161511449990764986292... (sequence A002117 in OEIS).
The reciprocal of this constant is the probability that any three positive integers, chosen at random, will be relatively prime (in the sense that as N goes to infinity, the probability that three positive integers less than N chosen uniformly at random will be relatively prime approaches this value).
Contents |
Apéry's theorem
This value was named for Roger Apéry (1916–1994), who in 1978 proved it to be irrational. This result is known as Apéry's theorem. The original proof is complex and hard to grasp, and shorter proofs have been found later, using Legendre polynomials. It is not known whether Apéry's constant is transcendental.
Work by Wadim Zudilin and Tanguy Rivoal has shown that infinitely many of the numbers ζ(2n+1) must be irrational,[1] and even that at least one of the numbers ζ(5), ζ(7), ζ(9), and ζ(11) must be irrational.[2]
Series representation
In 1772, Leonhard Euler (Euler 1773) gave the series representation (Srivastava 2000, p. 571 (1.11)):
which was subsequently rediscovered several times.
Ramanujan gives several series, which are notable in that they can provide several digits of accuracy per iteration. These include[3]:
Simon Plouffe has developed other series(Plouffe 1998):
Similar relations for the values of 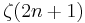 are given in the article zeta constants.
are given in the article zeta constants.
Many additional series representations have been found, including:
and
where
Some of these have been used to calculate Apéry's constant with several million digits.
Broadhurst (1998) gives a series representation that allows arbitrary binary digits to be computed, and thus, for the constant to be obtained in nearly linear time, and logarithmic space.
Other formulas
Apéry's constant can be expressed in terms of the second-order polygamma function as
It can be expressed as the non-periodic continued fraction [1; 4, 1, 18, 1, 1, 1, 4, 1, ...] (sequence A013631 in OEIS).
Known digits
The number of known digits of Apéry's constant ζ(3) has increased dramatically during the last decades. This is due both to the increase of performance of computers as well as to algorithmic improvements.
| Date | Decimal digits | Computation performed by |
|---|---|---|
| 1735 | 16 | Leonhard Euler |
| unknown | 16 | Adrien-Marie Legendre |
| 1887 | 32 | Thomas Joannes Stieltjes |
| 1996 | 520,000 | Greg J. Fee & Simon Plouffe |
| 1997 | 1,000,000 | Bruno Haible & Thomas Papanikolaou |
| May 1997 | 10,536,006 | Patrick Demichel |
| February 1998 | 14,000,074 | Sebastian Wedeniwski |
| March 1998 | 32,000,213 | Sebastian Wedeniwski |
| July 1998 | 64,000,091 | Sebastian Wedeniwski |
| December 1998 | 128,000,026 | Sebastian Wedeniwski (Wedeniwski 2001) |
| September 2001 | 200,001,000 | Shigeru Kondo & Xavier Gourdon |
| February 2002 | 600,001,000 | Shigeru Kondo & Xavier Gourdon |
| February 2003 | 1,000,000,000 | Patrick Demichel & Xavier Gourdon |
| April 2006 | 10,000,000,000 | Shigeru Kondo & Steve Pagliarulo (see Gourdon & Sebah (2003)) |
| January 2009 | 15,510,000,000 | Alexander J. Yee & Raymond Chan (see Yee & Chan (2009)) |
| March 2009 | 31,026,000,000 | Alexander J. Yee & Raymond Chan (see Yee & Chan (2009)) |
| September 2010 | 100,000,001,000 | Alexander J. Yee (see Yee) |
Notes
- ^ T. Rivoal (2000), "La fonction zeta de Riemann prend une infnité de valuers irrationnelles aux entiers impairs", Comptes Rendus Acad. Sci. Paris Sér. I Math. 331: 267–270.
- ^ W. Zudilin (2001), "One of the numbers ζ(5), ζ(7), ζ(9), ζ(11) is irrational", Russ. Math. Surv. 56 (4): 774–776, doi:10.1070/RM2001v056n04ABEH000427.
- ^ Bruce C. Berndt, Ramanujan's notebooks, Part II (1989), Springer-Verlag. See chapter 14, formulas 25.1 and 25.3
References
- Broadhurst, D.J. (1998), Polylogarithmic ladders, hypergeometric series and the ten millionth digits of ζ(3) and ζ(5), arXiv:math.CA/9803067
- Ramaswami, V. (1934), "Notes on Riemann's ζ-function", J. London Math. Soc. 9 (3): 165–169, doi:10.1112/jlms/s1-9.3.165
- Apéry, Roger (1979), "Irrationalité de ζ(2) et ζ(3)", Astérisque 61: 11–13
- A. van der Poorten (1979), "A proof that Euler missed..", The Mathematical Intelligencer 1 (4): 195–203, doi:10.1007/BF03028234, http://www.maths.mq.edu.au/~alf/45.pdf.
- Plouffe, Simon (1998), Identities inspired from Ramanujan Notebooks II, http://www.lacim.uqam.ca/~plouffe/identities.html
- Plouffe, Simon (undated), Zeta(3) or Apery constant to 2000 places, http://www.worldwideschool.org/library/books/sci/math/MiscellaneousMathematicalConstants/chap97.html
- Wedeniwski, S. (2001), Simon Plouffe, ed., The Value of Zeta(3) to 1,000,000 places, Project Gutenberg
- Srivastava, H. M. (December 2000), "Some Families of Rapidly Convergent Series Representations for the Zeta Functions" (PDF), Taiwanese Journal of Mathematics 4 (4): 569–598, OCLC 36978119, http://www.math.nthu.edu.tw/~tjm/abstract/0012/tjm0012_3.pdf, retrieved 2008-05-18
- Euler, Leonhard (1773), "Exercitationes analyticae" (in Latin) (PDF), Novi Commentarii academiae scientiarum Petropolitanae 17: 173–204, http://math.dartmouth.edu/~euler/docs/originals/E432.pdf, retrieved 2008-05-18
- Gourdon, Xavier; Sebah, Pascal (2003), The Apéry's constant: z(3), http://numbers.computation.free.fr/Constants/Zeta3/zeta3.html
- Weisstein, Eric W., "Apéry's constant" from MathWorld.
- Yee, Alexander J.; Chan, Raymond (2009), Large Computations, http://www.numberworld.org/nagisa_runs/computations.html
This article incorporates material from Apéry's constant on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.
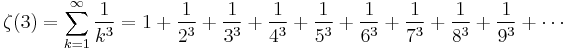
![\zeta(3)=\frac{\pi^2}{7}
\left[ 1-4\sum_{k=1}^\infty \frac {\zeta (2k)} {(2k%2B1)(2k%2B2) 2^{2k}} \right]](/2012-wikipedia_en_all_nopic_01_2012/I/36ed4a460f32293e1ce2e8a0489a368f.png)